The Screen representation of spin networks: 2D recurrence, eigenvalue equation for 6j symbols, geometric interpretation and Hamiltonian dynamics
Abstract
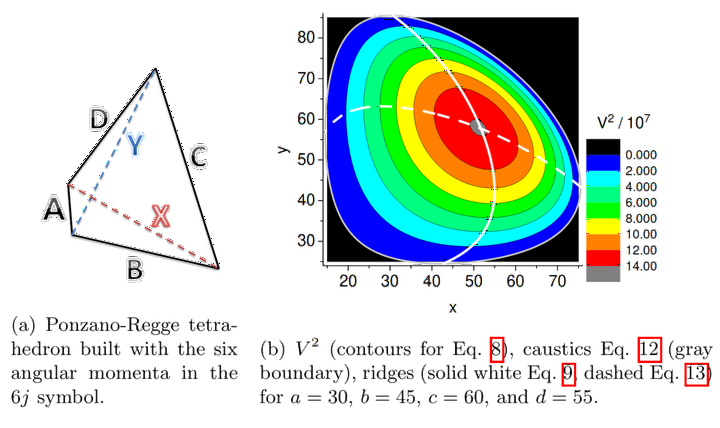
This paper treats 6j symbols or their orthonormal forms as a function of two variables spanning a square manifold which we call the “screen”. We show that this approach gives important and interesting insight. This two dimensional perspective provides the most natural extension to exhibit the role of these discrete functions as matrix elements that appear at the very foundation of the modern theory of classical discrete orthogonal polynomials. Here we present 2D and 1D recursion relations that are useful for the direct computation of the orthonormal 6j, which we name U. We present a convention for the order of the arguments of the 6j that is based on their classical and Regge symmetries, and a detailed investigation of new geometrical aspects of the 6j symbols. Specifically we compare the geometric recursion analysis of Schulten and Gordon with the methods of this paper. The 1D recursion relation, written as a matrix diagonalization problem, permits an interpretation as a discrete Shrödinger-like equations and an asymptotic analysis illustrates semiclassical and classical limits in terms of Hamiltonian evolution.