Spin-Coupling Diagrams and Incidence Geometry: A Note on Combinatorial and Quantum-Computational Aspects

Abstract

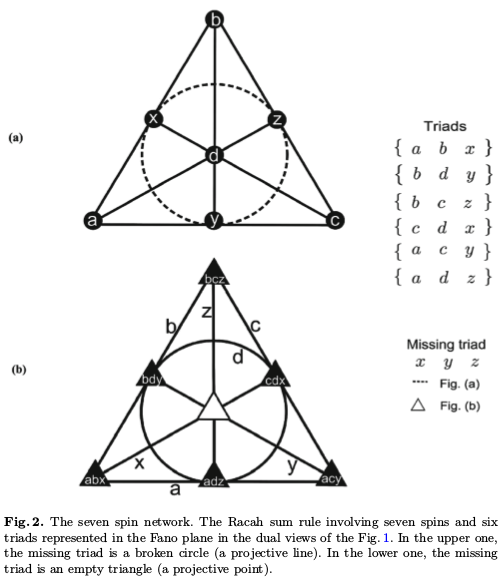
This paper continues previous work on quantum mechanical angular momentum theory and its applications. Relationships with projective geometry provide insight on various areas of physics and computational science. The seven-spin network previously introduced and the associate diagrams are contrasted to those of the Fano plane and its intriguing missing triad is discussed graphically. The two graphs are suggested as combinatorial and finite-geometrical “abacus” for quantum information applications, specifically for either (i)- a fermion-boson protocol, the hardware being typically a magnetic moiety distinguishing odd and even spins, or (ii)- a quantum-classical protocol, the hardware being materials (arguably molecular radicals) with both large and small angular momentum states.