Single and Collective Dynamics of Discretized Geometries
Abstract
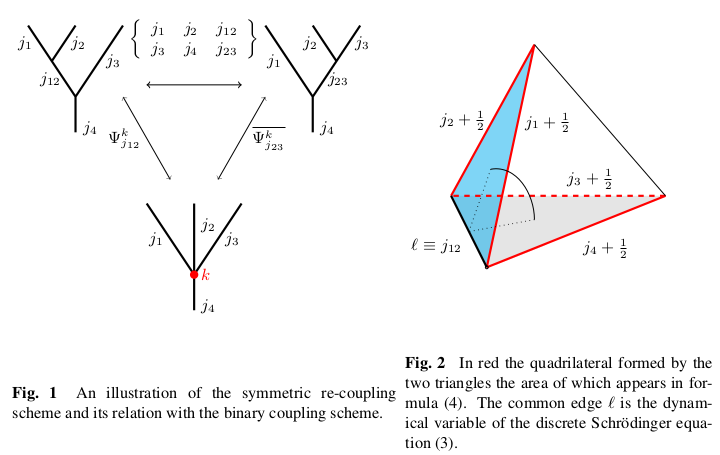
This paper reports a summary of the results of the PhD thesis. It is divided into two parts. In the first part the dynamics of the simplest ‘atom’ of space, emergent semiclassically from a purely quantum object called the volume operator, is studied. The associated three-terms recurrence relation and the family of orthogonal polynomials are described. In the second part, we study Lorentzian structures needed to build a discretized model of spacetime focusing on the topology $S^3 \times R$.
Publication
Scientifica Acta Vol 7 56-64
Date
March, 2014
Links
Bibtex:
@Article{marinelli2014single,
Title = {Single and Collective Dynamics of Discretized Geometries},
Author = {Marinelli, Dimitri},
Journal = {Scientifica Acta},
Year = {2014},
Number = {1},
Pages = {56-64},
Volume = {7},
}