Symmetric coupling of angular momenta, quadratic algebras and discrete polynomials

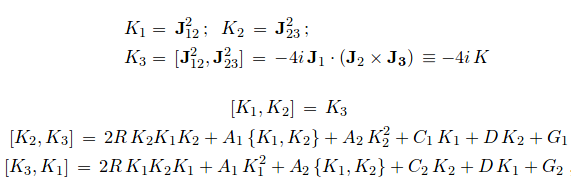
Abstract

Eigenvalues and eigenfunctions of the volume operator, associated with the symmetric coupling of three SU(2) angular momentum operators, can be analyzed on the basis of a discrete Schrödinger–like equation which provides a semiclassical Hamiltonian picture of the evolution of a ‘quantum of space’, as shown by the authors in [1]. Emphasis is given here to the formalization in terms of a quadratic symmetry algebra and its automorphism group. This view is related to the Askey scheme, the hierarchical structure which includes all hypergeometric polynomials of one (discrete or continuous) variable. Key tool for this comparative analysis is the duality operation defined on the generators of the quadratic algebra and suitably extended to the various families of overlap functions (generalized recoupling coefficients). These families, recognized as lying at the top level of the Askey scheme, are classified and a few limiting cases are addressed.

@Article{Aquilanti:2014gka,
  Title                    = {{Symmetric coupling of angular momenta, quadratic algebras and discrete polynomials}},
  Author                   = {Aquilanti, V. and Marinelli, D. and Marzuoli, A.},
  Journal                  = {Journal of Physics: Conference Series},
  Year                     = {2014},
  Pages                    = {012001},
  Volume                   = {482},

  Archiveprefix            = {arXiv},
  Booktitle                = {{Proceedings, Physics and Mathematics of Nonlinear Phenomena (PMNP 2013)}},
  Doi                      = {10.1088/1742-6596/482/1/012001},
  Eprint                   = {1401.3591},
  Primaryclass             = {quant-ph},
}